Giles Gardam

News: I have just uploaded a preprint to the arxiv disproving the unit conjecture in characteristic zero. Accompanying code is available in a zenodo repository.

Starting October 2023 I'm a professor of mathematics (Bonn Junior Fellow, temporary W2) at the University of Bonn, funded by my ERC Starting Grant SATURN. I was previously at the University of Münster (2019-2023), where I was awarded funding in the Emmy Noether programme of the DFG, and the Technion (2017-2018). I was a graduate student of Martin Bridson in Oxford and defended my DPhil thesis in 2017.

• Email: <last name>@math.uni-bonn.de
• Pronouns: he/him
• Pronunciation: dʒaɪlz starts like giant and rhymes with miles

This semester I'm teaching an advanced topics course on Group rings of infinite groups; the lecture notes are available online. I'm also organizing the GGT seminar.

Research interests

I work in geometric group theory, often from a computational perspective. A particular focus of my research (and ERC project) is the Kaplansky conjectures on group rings. Other topics include: one-relator groups, finiteness properties, profinite rigidity, minimal presentations, notions of non-positive curvature.

Group members

• Jonathan Fruchter (postdoc)
• Andrew Ng (PhD student)

Papers

My papers are all on my arXiv page.

Published or accepted for publication

• The Surface Group Conjectures for groups with two generators, with Dawid Kielak and Alan Logan, arXiv:2202.11093 journal version
  Math. Res. Lett. 30 (2023), 109–123
  abstract

  The Surface Group Conjectures are statements about recognising surface groups among one-relator groups, using either the structure of their finite-index subgroups, or all subgroups. We resolve these conjectures in the two generator case. More generally, we prove that every two-generator one-relator group with every infinite-index subgroup free is itself either free or a surface group.

• Alternative proof of ball-restricted version, appendix to the paper Two generalisations of Leighton's Theorem of S. Shepherd, joint with Daniel Woodhouse, arXiv:1908.00830 journal version
  Groups Geom. Dyn. 16 (2022), 743–778
• A counterexample to the unit conjecture for group rings, arXiv:2102.11818 journal version
  Ann. of Math. 194 (2021), 967–979
  quanta article - announcement talk - slides from NYGT talk
  abstract

  The unit conjecture, commonly attributed to Kaplansky, predicts that if \(K\) is a field and \(G\) is a torsion-free group then the only units of the group ring \(K[G]\) are the trivial units, that is, the non-zero scalar multiples of group elements. We give a concrete counterexample to this conjecture; the group is virtually abelian and the field is order two.

• Cannon–Thurston maps for CAT(0) groups with isolated flats, with Benjamin Beeker, Matthew Cordes, Radhika Gupta, and Emily Stark, arXiv:1810.13285 journal version
  Math. Ann. 384 (2022), 963–987
  abstract

  Mahan Mitra (Mj) proved Cannon–Thurston maps exist for normal hyperbolic subgroups of a hyperbolic group. We prove that Cannon–Thurston maps do not exist for infinite torsion-free normal hyperbolic subgroups of a non-hyperbolic CAT(0) group with isolated flats with respect to the visual boundaries. We also show Cannon–Thurston maps do not exist for infinite torsion-free infinite-index normal CAT(0) subgroups with isolated flats in a non-hyperbolic CAT(0) group with isolated flats. We determine the isomorphism types of the normal subgroups in the above two settings.

  
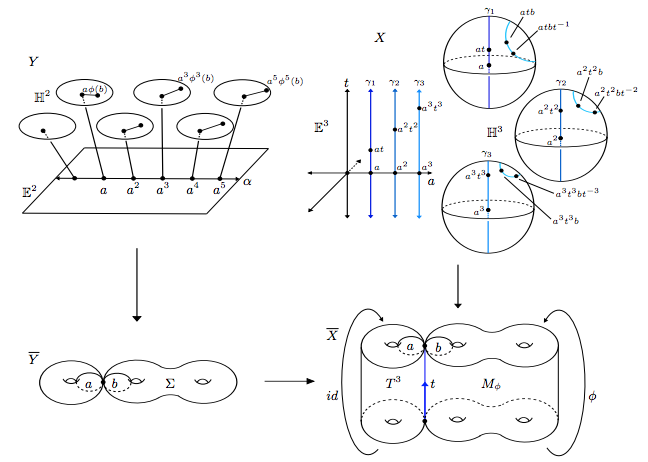
• Minimal sizeable graphs, appendix to the paper Hyperbolic Groups with Finitely Presented Subgroups not of Type F₃ of R. Kropholler, arXiv:1808.09505 journal version
  Geom. Dedicata 213 (2021), 589–619
  
• Profinite rigidity in the SnapPea census, arXiv:1805.02697 journal version
  Exp. Math. 30 (2021), 489-498
  (Note: arXiv version will be updated after embargo period from journal.)
  abstract

  A well-known question asks whether any two non-isometric finite volume hyperbolic 3-manifolds are distinguished from each other by the finite quotients of their fundamental groups. At present, this has been proved only when one of the manifolds is a once-punctured torus bundle over the circle. We give substantial computational evidence in support of a positive answer, by showing that no two manifolds in the SnapPea census of 72 942 finite volume hyperbolic 3-manifolds have the same finite quotients.

  
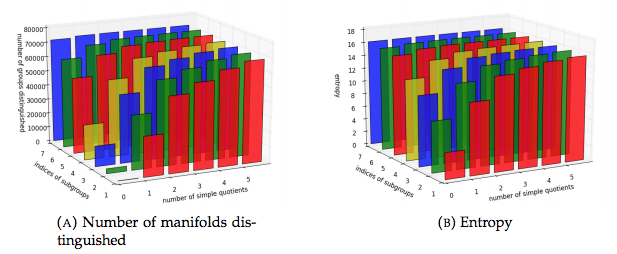
• Detecting laws in power subgroups, arXiv:1705.09348 journal version
  Comm. Algebra 47 (2019), 1699–1707
  (Note: arXiv version will be updated after embargo period from journal.)
  abstract

  A group law is said to be detectable in power subgroups if, for all coprime \(m\) and \(n\), a group \(G\) satisfies the law if and only if the power subgroups \(G^m\) and \(G^n\) both satisfy the law. We prove that for all positive integers \(c\), nilpotency of class at most \(c\) is detectable in power subgroups, as is the \(k\)-Engel law for \(k\) at most 4. In contrast, detectability in power subgroups fails for solvability of given derived length: we construct a finite group \(W\) such that \(W^2\) and \(W^3\) are metabelian but \(W\) has derived length \(3\). We analyse the complexity of the detectability of commutativity in power subgroups, in terms of finite presentations that encode a proof of the result.

  
• The geometry of one-relator groups satisfying a polynomial isoperimetric inequality with Daniel Woodhouse, arXiv:1711.08755 journal version
  Proc. Amer. Math. Soc. 147 (2019), 125–129
  abstract

  For every pair of positive integers \(p > q\) we construct a one-relator group \(R_{p,q}\) whose Dehn function is \(\simeq n^\alpha\) where \(\alpha = 2 \log_2(2p / q)\). The group \(R_{p,q}\) has no subgroup isomorphic to a Baumslag-Solitar group \(BS(m,n)\) with \(m \neq \pm n\), but is not automatic, not CAT(0), and cannot act freely on a CAT(0) cube complex. This answers a long-standing question on the automaticity of one-relator groups and gives counterexamples to a conjecture of Wise.

  
• Finite groups of arbitrary deficiency, arXiv:1705.02040 journal version
  Bull. London Math. Soc. 49 (2017), 1100–1104
  abstract

  The deficiency of a group is the maximum over all presentations for that group of the number of generators minus the number of relators. Every finite group has non-positive deficiency. We show that every non-positive integer is the deficiency of a finite group – in fact, of a finite \(p\)-group for every prime \(p\). This completes Kotschick's classification of the integers which are deficiencies of fundamental groups of compact Kähler manifolds.

  

Preprints

• Non-trivial units of complex group rings, arxiv:2312.05240
  abstract

  The Kaplansky unit conjecture for group rings is false in characteristic zero.

• Graphs and groups with unique geodesics, with Murray Elder, Adam Piggott, Davide Spriano and Kane Townsend, arxiv:2311.03730
  abstract

  A graph is called geodetic if there is a unique geodesic between each pair of vertices. Although natural objects, geodetic graphs remain mysterious and do not yet admit a satisfactory classification. In this paper we tackle the case of infinite graphs. We prove that if a locally finite quasi-transitive graph is geodetic, then it is quasi-isometric to a tree. From the group theoretic perspective, this implies that a finitely generated group that admits a geodetic Cayley graph is virtually free. Our main tool is to define a boundary and understand how local behaviour influences it. Our results unify, and represent significant progress on, programs of research initiated by Ore, Shapiro, and Madlener and Otto.

• Algebraically hyperbolic groups, with Dawid Kielak and Alan Logan, arXiv:2112.01331
  abstract

  We initiate the study of torsion-free algebraically hyperbolic groups; these groups generalise, and are intricately related to, groups with no Baumslag-Solitar subgroups. Indeed, for groups of cohomological dimension 2 we prove that algebraic hyperbolicity is equivalent to containing no Baumslag-Solitar subgroups. This links algebraically hyperbolic groups to two famous questions of Gromov; recent work has shown these questions to have negative answers in general, but they remain open for groups of cohomological dimension 2.

  We also prove that algebraically hyperbolic groups are CSA, and so have canonical abelian JSJ-decompositions. In the two-generated case we give a precise description of the form of these decompositions.

• JSJ decompositions and polytopes for two-generator one-relator groups, with Dawid Kielak and Alan Logan, arXiv:2101.02193
  abstract

  We provide a direct connection between the \(\mathcal{Z}_{\max}\) (or essential) JSJ decomposition and the Friedl–Tillmann polytope of a hyperbolic two-generator one-relator group with abelianisation of rank \(2\). We deduce various structural and algorithmic properties, like the existence of a quadratic-time algorithm computing the \(\mathcal{Z}_{\max}\)-JSJ decomposition of such groups.

In preparation

• Solving semidecidable problems in group theory
  talk at SMRI

Extended abstracts / technical reports (not peer reviewed)

• Computing fibrings
  Oberwolfach Reports 2020
• The Kaplansky conjectures
  Oberwolfach Reports 2022
• Group ring units in SAT
  Proceedings of SAT Competition 2022

Recent recorded talks

• SMRI Algebra and Geometry Online Seminar, 5 October 2021 (video)
• Global Noncommutative Geometry Seminar, 17 September 2021 (video)

Previous talks

Teaching

Where you might have met me

Other writing

• My doctoral thesis Encoding and Detecting Properties in Finitely Presented Groups (available for posterity via permalink at the Oxford University Research Archive)

• Expander Graphs and Kazhdan's Property (T), my 2012 Honours thesis at the University of Sydney

  

• I made some posters

• You can find me on Mastodon